[LeetCode]——爬楼梯

NO.70 爬楼梯 简单

思路一：深搜 超时

两种情况，走一层和走两层。触底返回。

public int climbStairs(int n) {
    switch (n){
        case 1:return 1;
        case 2:return 2;
    }
    return climbStairs(n-1)+climbStairs(n-2);
}

情况太多没做记忆化递归，就是个暴力。

思路二：动态规划

dp数组含义：dp[i]表示i阶有多少中走法。

初始化：dp[0]=1、dp[1]=1。

状态转移：dp[i]=dp[i-1]+dp[i-2]，第i阶是从i-1阶一次走一步上来和i-2阶一次走两步上来这两情况组成的。

public int climbStairs(int n) {
    int[] dp=new int[n+1];
    dp[0]=dp[1]=1;
    for (int i = 2; i <= n; i++) {
        dp[i]=dp[i-1]+dp[i-2];
    }
    return dp[n];
}

时间复杂度：O(n)

思路三：数学

从dp状态转移方程不难看出这是斐波那契数列，公式如下：

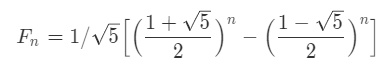
直接公式实现。

public int climbStairs(int n) {
    double sqrt_5 = Math.sqrt(5);
    double fib_n = Math.pow((1 + sqrt_5) / 2, n + 1) - Math.pow((1 - sqrt_5) / 2,n + 1);
    return (int)(fib_n / sqrt_5);
}

时间复杂度：O(logn)

---

本人菜鸟，有错误请告知，感激不尽！

更多题解和源码:github