[LeetCode]——x的平方根

NO.69 x的平方根简单

思路一：二分法

一个数的平方根一定不会大于这个数的一半，4的平方根2，8的平方根2.xxx。

也就是说我们只需要寻找[1,x/2]这个范围里的出就可以了，0单独判断，在确定的区间里二分查找。

left、right、mid、平方数都要用long类型防止大整形测试用例。

mid一定取右中位数，如果取左中位数，可能死循环。例如9，left=3，right=4，一直是9<9不成立进入left=mid这个分支，区间不发生收缩。

public int mySqrt(int x) {
    if (x==0)return 0;
    long left=1,right=x/2;
    while (left < right) {
        //取右中位数
        long mid=(left+right+1)>>>1;//(right-left+1)/2+left
        long square=mid*mid;
        if (square > x) {//向左收缩
            right=mid-1;
        }else {
            left=mid;
        }
    }
    return (int)left;
}

时间复杂度：O(logn)

思路二：牛顿迭代法

数学粉末直接搬运liweiwei1419大佬的讲解。

使用牛顿法可以得到一个正实数的算术平方根，因为题目中说“结果只保留整数部分”，因此，我们把使用牛顿法得到的浮点数转换为整数即可。

这里给出牛顿法的思想：

在迭代过程中，以直线代替曲线，用一阶泰勒展式（即在当前点的切线）代替原曲线，求直线与 xx 轴的交点，重复这个过程直到收敛。

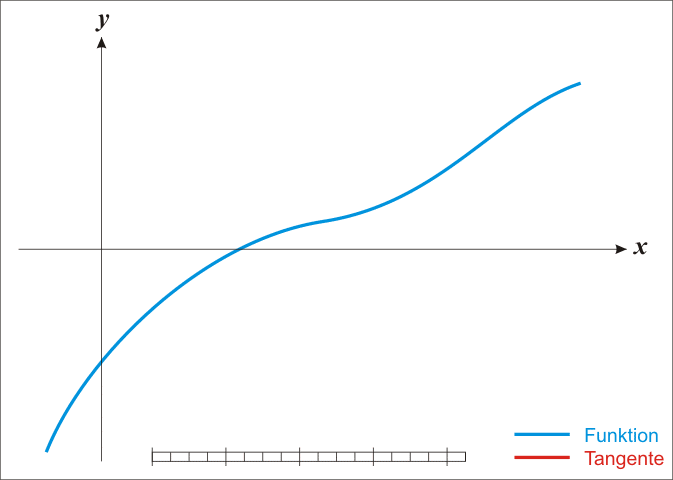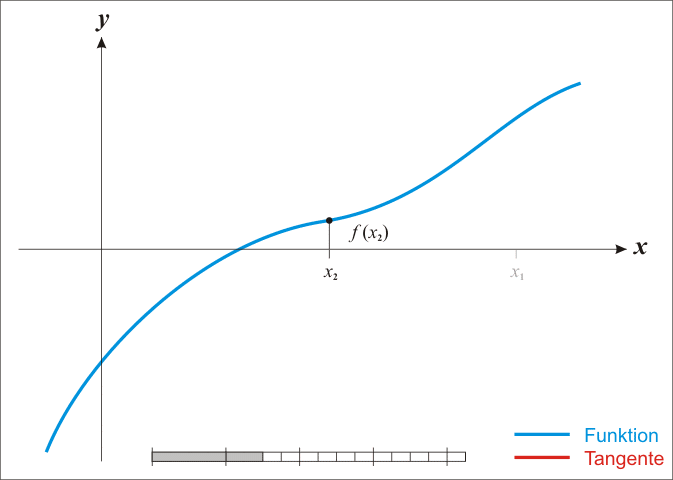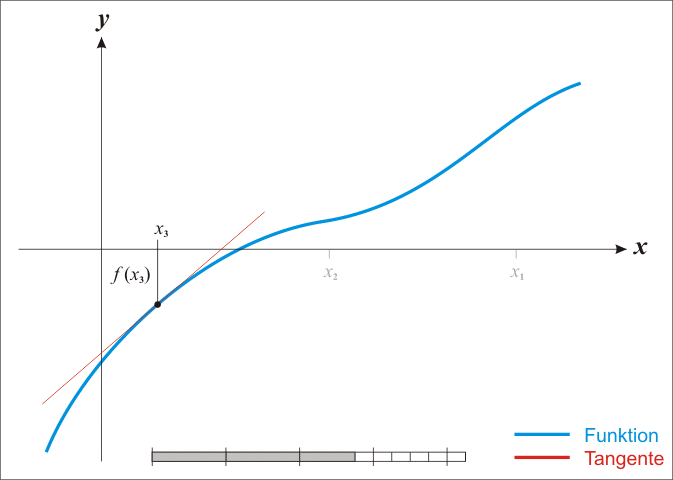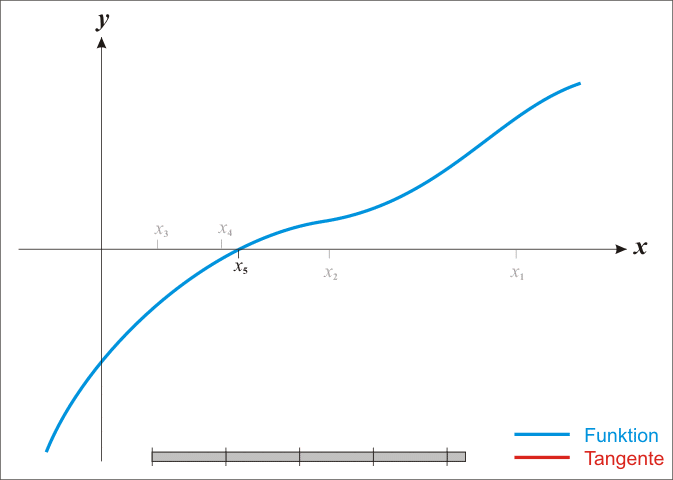
说明：

以上图片来自《牛顿法与拟牛顿法》；
题解《牛顿迭代法》的图和文字说明更好，而知乎问答《如何通俗易懂地讲解牛顿迭代法求开方？数值分析？》里面干货就更多了，建议大家出门左转观看，我这篇题解只是展示一下迭代公式如何计算。

注意：牛顿法得到的是平方根的浮点型精确值（可能会有一定误差），根据题目中的要求，把最后得到的这个数转换为 int 型，即去掉小数部分即可。

对“牛顿法”感兴趣的朋友们可以查一下牛顿法的应用：一个是求方程的根，另一个是求解最优化问题，在这里就不展开了。

public int mySqrt(int x) {
    long a=x;
    while (a * a > x) {
        a=(a+x/a)/2;
    }
    return (int)a;
}

说明：1e-6 是科学计数法，表示 11 乘以 1010 的负 66 次方，也就是 0.0000010.000001。有的地方使用 epsilon（ϵ）表示 1e-6 ，用来抵消浮点运算中因为误差造成的相等无法判断的情况，它通常是一个非常小的数字，具体多小要根据你的精度需求来设置。

本人菜鸟，有错误请告知，感激不尽！

更多题解和源码:github

NO.69 x的平方根 简单

思路一：二分法

思路二：牛顿迭代法

NO.69 x的平方根简单