LeetCode——实现Trie(前缀树)

NO.208 实现Trie(前缀树) 中等

思路一：实现前缀树 前缀树又名Trie树、字典树。举例说明：

例如有一些单词”A”, “to”, “tea”, “ted”, “ten”, “i”, “in”, “inn” ，要用字典树进行保存：

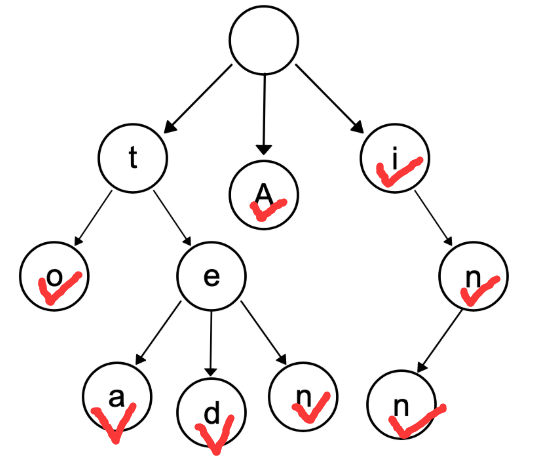
从根节点走到叶子节点，尝试走一下所有的路径。每条从根节点到叶子节点的路径都构成了单词（有的不需要走到叶子节点也是单词，比如 “i” 和 “in”）。trie树里的每个节点只需要保存当前的字符就可以了（当然你也可以额外记录别的信息，比如记录一下如果以当前节点结束是否构成单词、当前位置结尾的单词被搜索的次数等等）。

trie树是一个多叉树，这种特殊的多叉树的孩子节点数组的大小取决于字符集或者说是字符映射表（本题中要求的字符集是a-z，即大小是26）。

而且这种特殊的多叉树不需要保存每个节点的值，可以保存当前节点是否为一个单词串的结尾即可，还是因为有确定的字符集存在，这样通过父节点的next数组就可以映射出孩子节点的值。

//节点是否为单词串的结尾
private boolean isEnd;
//字符集是a-z
private Trie[] next;
private final int SIZE = 26;

public Trie() {
    this.isEnd = false;
    this.next = new Trie[SIZE];
}

插入：从根节点开始寻找和插入单词word第一个字符匹配的映射，如果映射下面有子树就继续寻找第二个字符匹配的映射，一直匹配到前缀链上没有对应的字符，这时开始不断开辟新的结点，直到插入完 word 的最后一个字符，同时还要将最后一个结点isEnd = true，表示它是一个单词的末尾。

public void insert(String word) {
    //拿到根节点
    Trie temp = this;
    //遍历word
    for (char c : word.toCharArray()) {
        //每个字符对应的next映射下没有子树
        if (temp.next[c - 'a'] == null) {
            //当前字符的映射下创建节点
            temp.next[c-'a']=new Trie();
        }
        //拿到下一个节点
        temp=temp.next[c-'a'];
    }
    //最后将字符映射到的最后一个节点设置为单词串的结尾
    temp.isEnd=true;
}

时间复杂度：O(n) word长度n

单词匹配：和插入的方式一样，区别在于当前缀链上没有对应的字符时返回false，找到完全匹配的前缀链后判断最后一个字符映射的节点是否为一个单词串的结尾。

public boolean search(String word) {
    //拿到根节点
    Trie temp=this;
    for (char c : word.toCharArray()) {
        //没有匹配的前缀链，false
        if (temp.next[c - 'a'] == null) {
            return false;
        }
        temp=temp.next[c-'a'];
    }
    //返回成功匹配的前缀链是否为一个单词串的结尾
    return temp.isEnd;
}

时间复杂度：O(n) word长度n

前缀匹配：和单词匹配一样，区别是最后不需要判断是否为一个单词的结尾。

public boolean startsWith(String prefix) {
    Trie temp=this;
    for (char c : prefix.toCharArray()) {
        if (temp.next[c - 'a'] == null) {
            return false;
        }
        temp=temp.next[c-'a'];
    }
    return true;
}

时间复杂度：O(n) 前缀长度n

简单学习了这个数据结构之后，做一下前缀树特点总结：

一次建树，多次查询。
Trie 的形状和单词的插入或删除顺序无关，也就是说对于任意给定的一组单词，Trie 的形状都是唯一的。
查找或插入一个长度为n的单词，访问 next 数组的次数最多为n+1，和 Trie 中包含多少个单词无关。
Trie 的每个结点中都保留着一个字母表(或者是字符集的表)，这是很耗费空间的。如果 Trie 的高度为 n，字母表的大小为 m，最坏的情况是 Trie 中还不存在前缀相同的单词，那空间复杂度就为 O(m^n)。

本人菜鸟，有错误请告知，感激不尽！

更多题解和源码:github