LeetCode——不同的二叉搜索树

NO.96 不同的二叉搜索树中等

思路一：动态规划

dp[i]的含义：n为i的时候搜索树有多少种。

初始化：大小为n+1，包含空树。dp[0]、dp[1]空树和只有1种。

状态转移：[1,n]区间中每个数字分别作为根节点，对于每个数字x作为根节点之后，它都是由左子树[1,x-1]和右子树[x+1,n]组成的，因此当x作为根节点的时候形成的不同的二叉搜索树有左子树*右子树种。

例如，n是4={“1作为根节点=左子树[1,0]*右子树[2,4]”+

“2作为根节点=左子树[1,1]*右子树[3,4]”+

“3做为根节点=左子树[1,2]*右子树[4,4]”+

“4作为根节点=左子树[1,3]*右子树[5,4]” }

public int numTrees(int n) {
    int[] dp=new int[n+1];
    dp[0]=dp[1]=1;
    //状态转移
    for (int i = 2; i < n + 1; i++) {
        //[1,i]中的i个数字分别做为根节点
        for (int j = 1; j < i+1; j++) {
            //左子树*右子树
            dp[i]+=dp[j-1]*dp[i-j];
        }
    }
    return dp[n];
}

时间复杂度：O(n^2)

思路二：卡塔兰数

事实上dp[n]的值被称为卡塔兰数 Cn。

卡塔兰数列的前几项为：

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, …[注： n = 0, 1, 2, 3, … n]

递推式：h(n)= h(0)*h(n-1) + h(1)*h(n-2) + … + h(n-1)*h(0) (其中n>=2)

——百度百科

卡塔兰数更便于计算的定义如下:

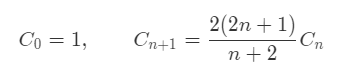
public int numTrees(int n) {
    long C=1;
    for (int i = 0; i < n; i++) {
        C=2*C*(2*i+1)/(i+2);
    }
    return (int)C;
}

时间复杂度：O(n)

本人菜鸟，有错误请告知，感激不尽！

更多题解和源码:github

NO.96 不同的二叉搜索树 中等

NO.96 不同的二叉搜索树中等