LeetCode——01矩阵

NO.542 01矩阵中等

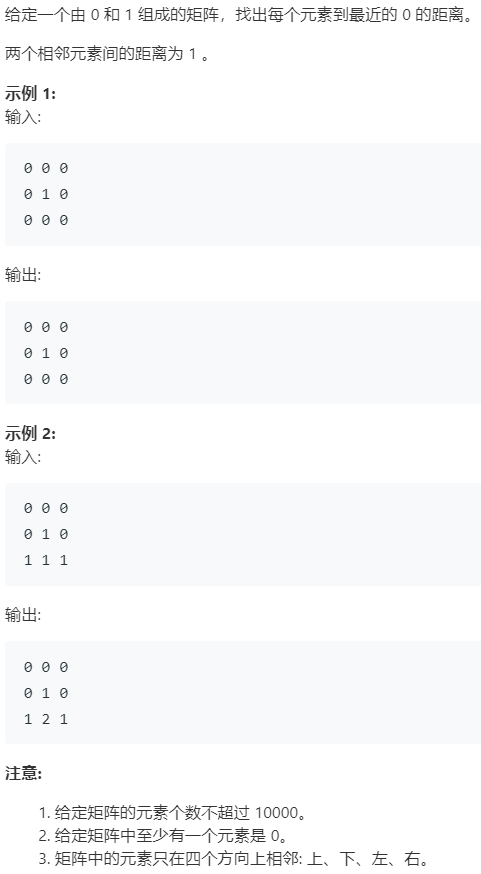
思路一：BFS 题干说找”最近的0的距离”，最短路问题第一个想法就是BFS。

找01矩阵中所有元素的距离0的位置：元素0和自身的距离是0，元素1和0的距离等于0到1的距离。

用一个标记数组记录每个位置是否已经计算过距离。

初始化结果集和队列，遍历矩阵找到所有等于0的位置，结果集对应位置赋值0并且坐标入队。计算过距离的位置标记。

广搜，队列中元素出队后向四个方向分别搜索一次寻找1(没有被标记过的位置就是1)，如果搜索位置存在1则记录结果集距离为结果集中搜索源点的值+1，并且入队、标记。

public int[][] updateMatrix(int[][] matrix) {
    if (matrix == null || matrix.length == 0) return null;
    int m = matrix.length, n = matrix[0].length;
    int[][] res = new int[m][n];//结果集
    boolean[][] visited = new boolean[m][n];//记录已经计算过的位置
    Queue<int[]> queue = new LinkedList<>();//广搜队列
    //遍历，将等于0的位置计入结果集并入队
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (matrix[i][j] == 0) {
                res[i][j] = 0;
                visited[i][j] = true;
                queue.offer(new int[]{i, j});
            }
        }
    }
    //四个方向广搜
    int[][] direction = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};//上下左右
    while (!queue.isEmpty()) {
        int[] poll = queue.poll();
        int i = poll[0], j = poll[1];
        //四个方向上找 1
        for (int k = 0; k < 4; k++) {
            int di = i + direction[k][0], dj = j + direction[k][1];
            //没有计算过的地方一定是 1
            if (di >= 0 && di < m && dj >= 0 && dj < n && !visited[di][dj]) {
                res[di][dj] = res[i][j] + 1;
                visited[di][dj] = true;
                queue.offer(new int[]{di, dj});
            }
        }
    }
    return res;
}

时间复杂度：O(n) 两次遍历

思路二：动态规划 其实在广搜思路中，就已经能从结果集中搜索源点的值+1这里尝到DP的味道了，再加上方法返回的这个距离数组需要逐步填表的过程，就能想到一些DP思路了。

dp[i][j]含义：就像题目中要求的matrix[i][j]距离0的最小距离。

初始化：dp数组元素赋一个最大值，遍历矩阵元素为0的地方先填写完毕。

状态转移：第一次遍历从左上到右下填表，每次只向右向下”搜索”；第二次遍历从右下到左上填表，每次只向左向上”搜索”。(有广搜内味了)

public int[][] updateMatrix(int[][] matrix) {
    if (matrix == null || matrix.length == 0) return null;
    int m = matrix.length, n = matrix[0].length;
    int[][] dp = new int[m][n];
    //初始化
    for (int i = 0; i < m; i++) {
        Arrays.fill(dp[i], 10001);
    }
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (matrix[i][j] == 0) dp[i][j] = 0;
        }
    }
    //状态转移
    //第一次填表从左上到右下
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (i - 1 >= 0) {
                dp[i][j] = Math.min(dp[i][j], dp[i - 1][j] + 1);
            }
            if (j - 1 >= 0) {
                dp[i][j] = Math.min(dp[i][j], dp[i][j - 1] + 1);
            }
        }
    }
    //第二次填表从右下到左上
    for (int i = m - 1; i >= 0; i--) {
        for (int j = n - 1; j >= 0; j--) {
            if (i + 1 < m) {
                dp[i][j] = Math.min(dp[i][j], dp[i + 1][j] + 1);
            }
            if (j + 1 < n) {
                dp[i][j] = Math.min(dp[i][j], dp[i][j + 1] + 1);
            }
        }
    }
    return dp;
}

时间复杂度：O(n) 初始化两次遍历，填表两次遍历。

本人菜鸟，有错误请告知，感激不尽！

更多题解和源码:github

NO.542 01矩阵 中等

NO.542 01矩阵中等