NO.127 单词接龙 中等

思路一:BFS
算是暴力吧,就是一次次遍历字典,找到可以转换的单词。
广搜免不了一个queue,再用一个数组记录被访问过的元素,不要重复判断。
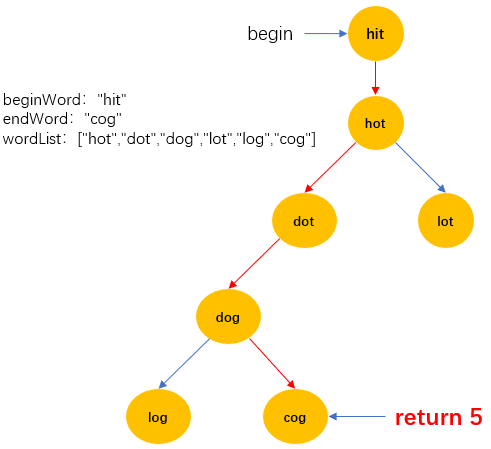
做一个逻辑结构形如上图树(不一定是二叉树)的层序遍历,孩子节点满足修改一个字符转换为父节点。根节点是beginWord,endWord是最后一个节点这个节点的所在深度+1作为结果。如果全部元素遍历完毕都没有找到endWord则返回0。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| public int ladderLength(String beginWord, String endWord, List<String> wordList) {
if (wordList == null || !wordList.contains(endWord)) return 0;
boolean[] isVisited = new boolean[wordList.size()];
Queue<String> queue = new LinkedList<>();
queue.add(beginWord);
int depth = 0;
while (!queue.isEmpty()) {
int size = queue.size();
depth++;
for (int i = 0; i < size; i++) {
String poll = queue.poll();
for (int j = 0; j < wordList.size(); j++) {
if (isVisited[j]) {
continue;
}
if (!canConvert(poll, wordList.get(j))) {
continue;
}
if (wordList.get(j).equals(endWord)) {
return depth + 1;
}
isVisited[j] = true;
queue.add(wordList.get(j));
}
}
}
return 0;
}
private boolean canConvert(String poll, String s) {
int count = 0;
for (int i = 0; i < s.length(); i++) {
if (poll.charAt(i) != s.charAt(i)) {
count++;
if (count > 1) {
return false;
}
}
}
return count == 1;
}
|
时间600+ms
时间复杂度不知道算的对不对:O(n^2) 层序遍历,每次弹出元素都要进行一次遍历list。
思路二:双向BFS
思路一是beginWord去找endWord,双向BFS思路是让begin和end相互寻找。为了让end可以去找begin,需要将beginWord也加入到wordList中。
依旧是按照思路一中的那个逻辑结构,从begin去找end。

与此同时再有一个同样的逻辑结构,从end去找begin。”cog”是根节点,”hit”是最终的目标节点。
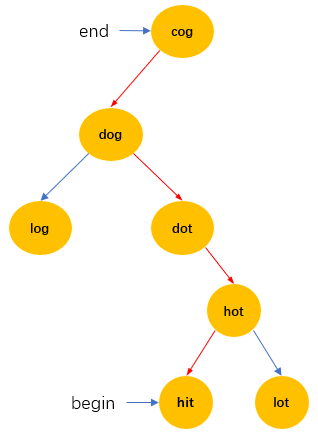
为什么要多此一举去增加一个end找begin呢?
答:不要着急,还需要对单向BFS返回条件做一些改变。
begin找end的A过程中,如果中间结点i已经被”end找begin”这条B支线访问过了,返回Adepth+Bdepth+1;
反之亦然,B的过程中,i被A访问过了,返回Adepth+Bdepth+1。
依旧是上例中,A过程遍历到深度为2的层,接下来B也将要遍历到深度为2的层,并且在这层会出现”dot”已经被A过程遍历第二层时访问过了,此时就叫做A过程和B过程在”dot”节点”碰头了”!则返回2+2+1=5。
看实现,虽然很长,但是思路清晰:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
| public int ladderLength(String beginWord, String endWord, List<String> wordList) {
if (wordList == null || !wordList.contains(endWord)) return 0;
wordList.add(beginWord);
int n = wordList.size();
int start = n - 1;
Set<Integer> visited1 = new HashSet<>();
Queue<Integer> queue1 = new LinkedList<>();
queue1.add(start);
visited1.add(start);
int depth1 = 0;
int end = wordList.indexOf(endWord);
Set<Integer> visited2 = new HashSet<>();
Queue<Integer> queue2 = new LinkedList<>();
queue2.add(end);
visited2.add(end);
int depth2 = 0;
while (!queue1.isEmpty() && !queue2.isEmpty()) {
depth1++;
int size1 = queue1.size();
while (size1-- > 0) {
String poll = wordList.get(queue1.poll());
for (int i = 0; i < n; i++) {
if (visited1.contains(i)) {
continue;
}
if (!canConvert(poll, wordList.get(i))) {
continue;
}
if (visited2.contains(i)) {
return depth1 + depth2 + 1;
}
visited1.add(i);
queue1.add(i);
}
}
depth2++;
int size2 = queue2.size();
while (size2-- > 0) {
String poll = wordList.get(queue2.poll());
for (int i = 0; i < wordList.size(); i++) {
if (visited2.contains(i)) {
continue;
}
if (!canConvert(poll, wordList.get(i))) {
continue;
}
if (visited1.contains(i)) {
return depth1 + depth2 + 1;
}
visited2.add(i);
queue2.add(i);
}
}
}
return 0;
}
private boolean canConvert(String poll, String s) {
int count = 0;
for (int i = 0; i < s.length(); i++) {
if (poll.charAt(i) != s.charAt(i)) {
count++;
if (count > 1) {
return false;
}
}
}
return true;
}
|
改为双向BFS后,时间800+ms。。。
接下来开始对双向BFS进行优化。
从AB两个方向的中,选择当前节点更少的队列,进行层序遍历。
修改后BFS部分实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| int depth = 0;
while (!queue1.isEmpty() && !queue2.isEmpty()) {
if (queue1.size() > queue2.size()) {
Queue<Integer> temp = queue1;
queue1 = queue2;
queue2 = temp;
Set<Integer> set = visited1;
visited1 = visited2;
visited2 = set;
}
depth++;
int size = queue1.size();
while (size-- > 0) {
String poll = wordList.get(queue1.poll());
for (int i = 0; i < wordList.size(); i++) {
if (visited1.contains(i)) {
continue;
}
if (!canConvert(poll, wordList.get(i))) {
continue;
}
if (visited2.contains(i)) {
return depth + 1;
}
visited1.add(i);
queue1.add(i);
}
}
}
|
BFS部分修改后,时间120+ms。。。
最后优化canConvert()方法,当前实现是将单词逐一进行比较,执行受单词数量的影响较大。
更好的实现思路:将队列弹出单词的每个字符,用区间[a,z]中的元素逐一进行替换,将替换后的新单词到字典中查找是否存在。由于[a,z]区间大小是常数,所以这个方法的执行主要受到单词长度的影响较大。并将字典用HashSet保存,这样每次判断时查找的速度更快。
因为单词大多都不会很长,但是字典中单词的数量经常很大。所以这种场景下,新思路会更好。
最终实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
| public int ladderLength(String beginWord, String endWord, List<String> wordList) {
if (wordList == null || !wordList.contains(endWord)) return 0;
wordList.add(beginWord);
Queue<String> queue1 = new LinkedList<>();
Set<String> visited1 = new HashSet<>();
queue1.add(beginWord);
visited1.add(beginWord);
Queue<String> queue2 = new LinkedList<>();
Set<String> visited2 = new HashSet<>();
queue2.add(endWord);
visited2.add(endWord);
int depth = 0;
Set<String> allWord = new HashSet<>(wordList);
while (!queue1.isEmpty() && !queue2.isEmpty()) {
if (queue1.size() > queue2.size()) {
Queue<String> temp = queue1;
queue1 = queue2;
queue2 = temp;
Set<String> set = visited1;
visited1 = visited2;
visited2 = set;
}
depth++;
int size = queue1.size();
while (size-- > 0) {
String poll = queue1.poll();
char[] chars = poll.toCharArray();
for (int i = 0; i < chars.length; i++) {
char temp = chars[i];
for (char c = 'a'; c <= 'z'; c++) {
chars[i] = c;
String newString = new String(chars);
if (visited1.contains(newString)) {
continue;
}
if (visited2.contains(newString)) {
return depth + 1;
}
if (allWord.contains(newString)) {
queue1.add(newString);
visited1.add(newString);
}
}
chars[i] = temp;
}
}
}
return 0;
}
|
最终运行时间20+ms!
时间复杂度:O(n*len) n单词个数,len单词长度。
空间复杂度:O(n)
本人菜鸟,有错误请告知,感激不尽!
更多题解和源码:github



