长大后想做什么？做回小孩！

0%

LeetCode——只出现一次的数字I&II&III

发表于 分类于 Valine：
本文字数： 687

只出现一次的数字 简单、只出现一次的数字II 中等、只出现一次的数字III 中等

NO.136 只出现一次的数字 简单

JOK1BR.png

思路一：异或

1
2
3
4
5
6
7
public int singleNumber(int[] nums) {
    int ans = 0;
    for (int num : nums) {
        ans^=num;
    }
    return ans;
}

时间复杂度：O(n) 空间复杂度：O(1)

NO.137 只出现一次的数字II 中等

JOKGAx.png

思路一：按位统计 遍历数组中每个元素的每一位(除了符号位)，统计每一位上 1 的个数，最后再将每一位上 1的数量取模 3，得到最终的结果。例如：

1
2
3
nums[2,2,3,2]=nums[0010,0010,0011,0010]
统计每一位上1的次数：0041
每一位上的数字取模3：0011 = 3

不难理解，剩下的就是如何实现。

对每个数字 num 的右移待统计位数，再对 1 求与，可以得到待统计位上的是 1 还是 0。

统计完某一位上 1 的数量之后，取模 3 结果一定是 1 或 0 ，再左移回原本的位上，最后通过异或运算存到结果中。还是上例：

1
2
3
4
5
6
nums[2,2,3,2]=nums[0010,0010,0011,0010]
统计第0位上1的次数：1	取模3左移回到原位：0001	异或存回res：0001
统计第1位上1的次数：4	取模3左移回到原位：0010	异或存回res：0011
统计第3位上1的次数：0	取模3左移回到原位：0000	异或存回res：0011
统计第4位上1的次数：0	取模3左移回到原位：0000	异或存回res：0011
    最终结果res：0011 = 3
1
2
3
4
5
6
7
8
9
10
11
12
13
public int singleNumber(int[] nums) {
    int res = 0;
    //分别统计每一位上 1 的个数
    for (int i = 0; i < 32; i++) {
        int count = 0;
        for (int num : nums) {
            count += (num >> i) & 1;
        }
        //个数取模 3 再还原回原位,最后保存至res
        res ^= (count % 3) << i;
    }
    return res;
}

时间复杂度：O(n) 32次遍历O(32n)。

空间复杂度：O(1)

NO.260 只出现一次的数字III 中等

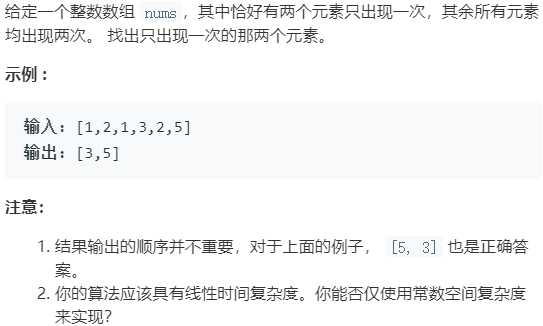
JOK3H1.png

思路一：分组异或 剑指Offer 第 56 题一样。

如果只有一个数字出现过一次，直接将数组遍历依次异或，最终的到的结果就是只出现过一次的数字。因为异或运算，相同为 0，不同为 1。

但是本题有两个只出现一次的数字 a、b，按照上述方法得到的结果一定是a^b。

如果可以将 nums 分为两组， a 和 b分别再不同的组，其余相同的元素一定在同一个组。这样，我们就可以像开头提到的方法一样，将两组分别异或，两组最后得到的结果，一定就是 a 和 b 。

重点在于如何分组：

  1. 先将 nums 遍历依次异或，得到 res=a^b。
  2. 与运算，拿到 res 任意一个等于 1 的位 h。
  3. 遍历 nums 分别和 h 进行与运算，等于 0 的分一组进行异或，不等于 0 的分一组进行异或，最后两组的结果就是 a 和 b。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public int[] singleNumber(int[] nums) {
    //得到 a^b
    int n = 0;
    for (int num : nums) {
        n ^= num;
    }
    //得到n中任意一位1的位置
    int h = 1;
    while ((h & n) == 0) {
        h <<= 1;
    }
    //分组异或
    int a = 0, b = 0;
    for (int num : nums) {
        if ((num & h) == 0) {
            a ^= num;
        } else {
            b ^= num;
        }
    }
    return new int[]{a, b};
}

时间复杂度：O(n) 空间复杂度：O(1)

本人菜鸟，有错误请告知，感激不尽！

更多题解和源码:github