单周速通《剑指Offer》I

数组中重复的数字 简单 、二维数组中的查找 简单 、替换空格 简单 、从尾到头打印链表 简单 、重建二叉树 中等 、用两个栈实现队列 简单 、斐波那契数列 简单、青蛙跳台阶 简单 旋转数组的最小数字 简单 、矩阵中的路径 中等

刷了有二百多道 LeetCode 了，听说找实习必刷《剑指Offer》，于是每天花一点时间把这套题速刷一遍。

如果有和我一样的菜鸟，咱们可以一起组队刷题，相互监督打卡哦！！干就完了！！！奥利给！！！！！

剑指Offer.03 数组中重复的数字 简单

思路一：HashTable 简单直白，遍历数组，用 HashSet 保存遇到过的元素，遇到重复就返回。

//时间复杂度：O(n)    空间复杂度：O(n)
public int findRepeatNumber(int[] nums) {
    Set<Integer> set = new HashSet<>();
    for (int num : nums) {
        if (set.contains(num)) {
            return num;
        } else {
            set.add(num);
        }
    }
    return -1;
}

思路二：抽屉定理 本文数组元素都小于数组长度，一个萝卜一个坑，将元素都放回自己的位置，期间遇到重复的元素就返回。类似于 LeetCode 41 题——缺失的第一个正数 。

//时间复杂度：O(n)    空间复杂度：O(1)
public int findRepeatNumber(int[] nums) {
    for (int i = 0; i < nums.length; i++) {
        while (nums[i] != i) {
            if (nums[i] == nums[nums[i]]) return nums[i];
            int temp = nums[i];
            nums[i] = nums[temp];
            nums[temp] = temp;
        }
    }
    return -1;
}

剑指Offer.04 二维数组中的查找 简单

思路一：双指针法，每次排除一行或一列 从左下角开始遍历 i 表示行坐标、j 表示列坐标，如果遇到等于 target 则返回 true，如果遍历元素大于 target ，因为每一行都是增序所以 i– 排除当前行，如果遍历元素小于 target ，因为每一列也都是从上到下增序的，所以 j++ 排除当前列。

//时间复杂度：O(m+n) m行，n列    空间复杂度：O(1)
public boolean findNumberIn2DArray(int[][] matrix, int target) {
    if (matrix.length == 0) return false;
    int m = matrix.length, n = matrix[0].length;
    int i = m - 1, j = 0;
    while (i >= 0 && j < n) {
        if (matrix[i][j] < target) {
            j++;
        } else if (matrix[i][j] > target) {
            i--;
        } else if (matrix[i][j] == target) {
            return true;
        }
    }
    return false;
}

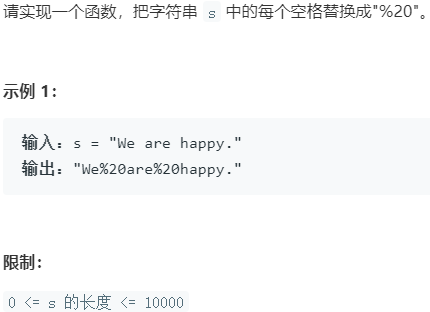
剑指Offer.05 替换空格 简单

思路一：直接遍历替换 没什么好说的遍历就完了！

//时间复杂度：O(n)    空间复杂度：O(n)
public String replaceSpace(String s) {
    StringBuilder res = new StringBuilder();
    for (char c : s.toCharArray()) {
        if (c != ' ') {
            res.append(c);
        }else {
            res.append("%20");
        }
    }
    return res.toString();
}

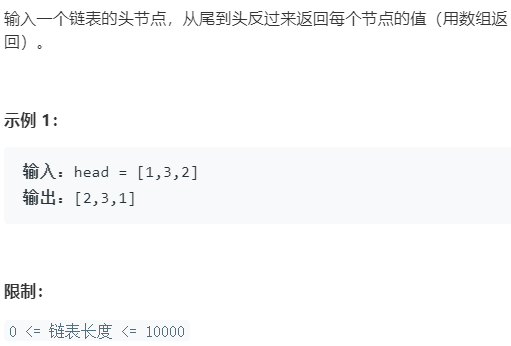
剑指Offer.06 从尾到头打印链表 简单

思路一：利用栈 逆序打印，那就是遍历节点入栈，再依次出栈，利用栈先进后出的特点。

//时间复杂度：O(n)    空间复杂度：O(n)
public int[] reversePrint(ListNode head) {
    Deque<ListNode> stack = new LinkedList<>();
    while (head != null) {
        stack.push(head);
        head = head.next;
    }
    int[] res = new int[stack.size()];
    for (int i = 0; i < res.length; i++) {
        res[i] = stack.pop().val;
    }
    return res;
}

思路二：递归，利用方法调用栈 可以不用手动创建一个栈，直接利用递归压栈，触底返回就好了。

//时间复杂度：O(n)    空间复杂度：O(n)
ArrayList<Integer> list = new ArrayList<>();

public int[] reversePrint(ListNode head) {
    recusion(head);
    int[] res = new int[list.size()];
    for (int i = 0; i < res.length; i++) {
        res[i] = list.get(i);
    }
    return res;
}

private void recusion(ListNode head) {
    if (head == null) return;
    recusion(head.next);
    list.add(head.val);
}

剑指Offer.07 重建二叉树 中等

思路一：先序找根，中序找到根的左右子树区间

回想了一下学校老师上课讲的如何根据两个遍历序列还原出二叉树的：

1. 根据前序序列的第一个字符确定树的根，示例中的3。
2. 知道了3这个根，根据中序序列确定左右子树[9]是左子树、[15,20,7]是右子树。
3. 根据左子树前序序列第一个字符确定树的根：9。9的左右子树为null，左子树完毕。
4. 根据右子树前序序列第一个字符确定树的根：20。
5. 知道了20这个根，根据中序序列确定左右子树[15]是左子树、[7]是右子树。
6. 根据左子树前序序列第一个字符确定树的根：15。15的左右子树为null，左子树完毕。
7. 根据右子树前序序列第一个字符确定树的根：7。7的左右子树为null，左子树完毕。

这个过程就是在利用：前序序列[根左右]根在开头确定根、中序遍历[左根右]确定根的左右子树。

实现的过程其实就是：先根据前序序列确定根，再根据中序序列确定根的左子树or右子树，再将左子树or右子树对应的前序序列区间和中序序列区间重复前两步。。。。

明显是个递归结构，递归出口是：前序或中序序列的区间为空。

可以用一个 Map 保存每个中序序列元素的下标，方便直接找到根节点在中序序列的位置，从而计算出左右子树的区间。如果不用 Map 每次都需要遍历一下中序序列的区间，才能找到根节点的位置。

//时间复杂度：O(n)    空间复杂度：O(n)
HashMap<Integer, Integer> map = new HashMap<>();

public TreeNode buildTree(int[] preorder, int[] inorder) {
    if (preorder.length != inorder.length) return null;
    for (int i = 0; i < inorder.length; i++) {
        map.put(inorder[i], i);
    }
    return build(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1);
}

private TreeNode build(int[] preorder, int pstart, int pend, int[] inorder, int istart, int iend) {
    if (pstart > pend || istart > iend) return null;
    if (pstart == pend) return new TreeNode(preorder[pstart]);
    TreeNode root = new TreeNode(preorder[pstart]);
    int rootIdx = map.get(preorder[pstart]);
    int leftOffset = rootIdx - istart, rightOffset = iend - rootIdx;
    root.left = build(preorder, pstart + 1, pstart + leftOffset, inorder, istart, rootIdx - 1);
    root.right = build(preorder, pend - rightOffset + 1, pend, inorder, rootIdx + 1, iend);
    return root;
}

剑指Offer.09 用两个栈实现队列 简单

思路一：保持主栈的顺序 每次入栈前都先将主栈(A)中的所有元素都出栈再入栈到辅助栈(B)中，然后新元素就能放到 A栈 的底部，新元素入栈之后再将 B栈 中的元素都出栈再入栈回 A栈。这样就能保证 A栈 中新入栈的元素都在栈底，最早的元素在栈顶。

public class CQueue {
    Deque<Integer> stackA, stackB;
    int size;

    public CQueue() {
        this.stackA = new LinkedList<>();
        this.stackB = new LinkedList<>();
        this.size = 0;
    }

    //时间复杂度：O(n)
    public void appendTail(int value) {
        while (!stackA.isEmpty()) {
            stackB.push(stackA.pop());
        }
        stackA.push(value);
        while (!stackB.isEmpty()) {
            stackA.push(stackB.pop());
        }
        size++;
    }

    //时间复杂度：O(1)
    public int deleteHead() {
        if (size == 0) {
            return -1;
        }
        size--;
        return stackA.pop();
    }
}

剑指Offer.10_I 斐波那契数列 简单

思路一：动态规划 学习 DP 的经典入门例题，一般会从暴力递归到记忆化递归最终到 DP，因为本文只是一个菜鸟的速通日记，介于篇幅就不展开了，直接给出空间压缩后的 DP 解法，下一题给出 DP 思考过程。

//时间复杂度：O(n)    空间复杂度：O(1)
public int fib(int n) {
    int a = 0, b = 1, sum = 0;
    for (int i = 1; i <= n; i++) {
        sum = (a + b) % 1000000007;
        a = b;
        b = sum;
    }
    return a;
}

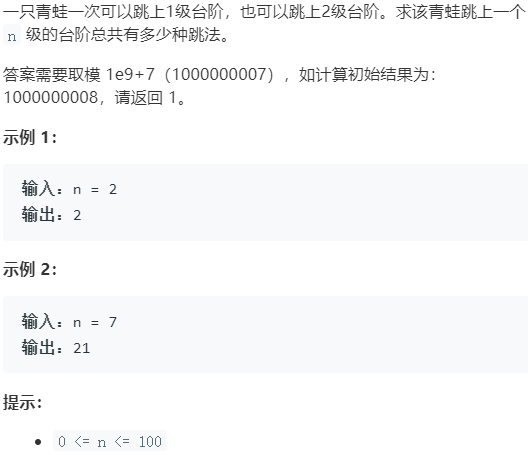
剑指Offer.10_II 青蛙跳台阶 简单

思路一：动态规划 和斐波契数列一样，区别是斐波那契数列是从 0,1,1,2,3。。。开始的，而本题的数列是从 1,1,2,3。。。开始的。

dp数组含义：dp[i]表示i阶有多少中走法。

初始化：dp[0]=1、dp[1]=1，即 0 阶 和 1阶都只有一种走法。

状态转移：dp[i]=dp[i-1]+dp[i-2]，第i阶是从i-1阶一次走一步上来和i-2阶一次走两步上来这两情况组成的。

//时间复杂度：O(n)    空间复杂度：O(n)
public int climbStairs(int n) {
    int[] dp=new int[n+1];
    dp[0]=dp[1]=1;
    for (int i = 2; i <= n; i++) {
        dp[i]=dp[i-1]+dp[i-2];
    }
    return dp[n];
}

因为计算 dp[i] 的时候，只考虑 dp[i-1] 和 dp[i-2] 所以用两个变量记录这两个值即可。

//时间复杂度：O(n)    空间复杂度：O(n)
public int numWays(int n) {
    int a = 1, b = 1, sum = 0;
    for (int i = 0; i < n; i++) {
        sum = (a + b) % 1000000007;
        a = b;
        b = sum;
    }
    return a;
}

剑指Offer.11 旋转数组的最小数字 简单

思路一：二分法 重点在于如何判断 mid 的条件？

用 nums[mid] 和 nums[right] 进行比较 ，如果 nums[mid] > nums[right] ，说明 mid 的左边部分一定是一个严格升序区间，那么最小值一定在 mid 右边的部分；反之 nums[mid] < nums[right] 说明 mid 的右边是一个严格升序全进，最小值一定在 mid 的左边部分；如果 nums[mid] = nums[right] ，说明发生重复，right– 跳过这个重复的值，继续判断。

搜索的时候，搜索区间不断地向存在最小值的那一边收缩，搜索区间选择左闭右闭区间，搜索停止条件是搜索区间内只剩下一个元素。

//最坏时间复杂度：O(n) 元素全部相同，退化到 O(n)
//平均时间复杂度：O(logn)
public int minArray(int[] numbers) {
    int left = 0, right = numbers.length - 1;
    //left == right 时停止搜索,此时左闭右闭区间内剩余一个元素
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (numbers[mid] == numbers[right]) {
            //跳过重复
            right--;
        } else if (numbers[mid] > numbers[right]) {
            //此时 mid 一定不是最小值,所以从搜索区间内删除
            left = mid + 1;
        } else if (numbers[mid] < numbers[right]) {
            right = mid;
        }
    }
    return numbers[left];
}

剑指Offer.12 矩阵中的路径 中等

思路一：深搜回溯 遍历board找到等于word第一个字符的元素。然后以这个元素为开始，向四个方向上分别进行递归深搜，如果某个方向上成功匹配整个word则返回true，如果某个元素四个方向都不能匹配成功word的对应字符则返回false。

因为字符不能重复使用，所以需要一个标记数组对每个字符的使用情况进行标记。也可以采用NO.695岛屿最大面积中的”沉岛思想”，将用过的字符直接修改为’.’。

//是否成功搜索word
boolean finished = false;

public boolean exist(char[][] board, String word) {
    //遍历
    for (int i = 0; i < board.length; i++) {
        for (int j = 0; j < board[0].length; j++) {
            //如果等于word第一个字符的元素，以i j 开始进行四个方向深搜
            if (board[i][j] == word.charAt(0) && dfs(board, word, i, j, 0)) {
                return true;
            }
        }
    }
    return false;
}

private boolean dfs(char[][] board, String word, int i, int j, int curr) {
    //匹配成功的长度等于word长度，成功搜索
    if (curr == word.length()) {
        finished = true;
        return true;
    }
    //如果到的边界或者字符不匹配
    if (i < 0 || i >= board.length || j < 0 || j >= board[0].length ||
        board[i][j] != word.charAt(curr)) {
        return false;
    }
    //当前未完成匹配，继续四个方向深搜
    if (!finished) {
        char c = board[i][j];//保存当前字符，回溯的时候重新填写回去
        board[i][j] = '.';//沉岛
        boolean down = dfs(board, word, i + 1, j, curr + 1);//向下搜
        boolean right = dfs(board, word, i, j + 1, curr + 1);//向右搜
        boolean up = dfs(board, word, i - 1, j, curr + 1);//向上搜
        boolean left = dfs(board, word, i, j - 1, curr + 1);//向左搜
        board[i][j] = c;//回溯重新将字符填回去
        return down || right || up || left;
    } else {
        return true;//已完成
    }
}

时间复杂度：O(mn*3^K) 最坏情况：有m*n个起点，每个起点都要遍历一个 word长度k的方案，除去上一个字符，还有 3 个方向

空间复杂度：O(k)递归调用栈不超过 k 层深度

---

本人菜鸟，有错误请告知，感激不尽！

更多题解源码和学习笔记：github 、CSDN 、M1ng