单周速通《剑指Offer》II

矩阵中的路径中等、剑指Offer.14_I 剪绳子中等、剑指Offer.14_II 剪绳子II 中等、剑指Offer.15 二进制中 1 的个数简单、剑指Offer.16 数值的整数次方中等、剑指Offer.17 打印从 1 到最大的 n 位数简单、剑指Offer.18 删除链表的节点简单、剑指Offer.19 正则表达式匹配困难、剑指Offer.20 表示数值的字符串中等、剑指Offer.21 调整数组顺序使奇数位于偶数前面简单、剑指Offer.22 链表中倒数第 k 个节点简单、剑指Offer.24 翻转链表简单、剑指Offer.25 合并两个排序的链表简单

剑指Offer.13 机器人的运动范围中等

题目中有一个计算横纵坐标数位之和的操作，这不是题目的关键点，将这个计算数位之和的方法封装起来不要干扰主要的解题逻辑。

public int sums(int x,int y){
    int ans=0;
    while (x != 0) {
        ans+=x%10;
        x/=10;
    }
    while (y != 0) {
        ans+=y%10;
        y/=10;
    }
    return ans;
}

思路一：深搜

想法比较直接，就是从起点开始用深搜的方式遍历矩阵，控制深搜边界的同时判断当前访问的位置数位和是否小于等于k，并且需要一个标记数组记录每个位置的访问情况，防止重复计算。

虽然题目说是上下左右都可以移动，但是我们从左上角作为起点开始只能向右或者向下移动，如果发生向左或者向上那一定是重复的搜索。

int m,n,k;
public int movingCount(int m, int n, int k) {
    this.m=m;
    this.n=n;
    this.k=k;
    //标记访问过的位置
    boolean[][] visited=new boolean[m][n];
    return dfs(0,0,0,visited);
}

/**
     * 深搜
     * @param i 横坐标
     * @param j 纵坐标
     * @param sum   坐标数位和
     * @param visited   标记数组
     * @return
     */
private int dfs(int i, int j, int sum, boolean[][] visited) {
    //如果 坐标越界 或者 数位和大于k 或者 已经访问过，则停止当前方向的深搜
    if (i==m||j==n||sum>k||visited[i][j])return 0;
    //标记为已访问
    visited[i][j]=true;
    //向下或者向右深搜
    return 1+dfs(i+1,j,sums(i+1,j),visited)+dfs(i,j+1,sums(i,j+1),visited);
}

//计算数位和
public int sums(int x,int y){
    int ans=0;
    while (x != 0) {
        ans+=x%10;
        x/=10;
    }
    while (y != 0) {
        ans+=y%10;
        y/=10;
    }
    return ans;
}

时间复杂度：O(mn) 最坏情况，遍历矩阵。

空间复杂度：O(mn)

思路二：广搜

其实和深搜的思路一样，只是换了一个搜索的方式，采用广搜的方式寻找符合要求的位置。

//时间复杂度：O(mn)
public int movingCount(int m, int n, int k) {
    //队列保存坐标
    Queue<int[]> queue=new ArrayDeque<>();
    //标记数组
    boolean[][] visited=new boolean[m][n];
    //广搜
    queue.add(new int[]{0,0});
    int count=0;
    visited[0][0]=true;
    while (!queue.isEmpty()) {
        int[] poll = queue.poll();
        count++;
        //向下、向右寻找符合要求的位置入队并标记访问状态
        //不越界 并且 数位和小于等于k 并且 未访问过
        if (poll[0] + 1 < m
            && sums(poll[0] + 1, poll[1]) <= k
            &&!visited[poll[0]+1][poll[1]]){
            queue.add(new int[]{poll[0]+1,poll[1]});
            visited[poll[0]+1][poll[1]]=true;
        }
        if (poll[1] + 1 < n
            && sums(poll[0], poll[1] + 1) <= k
            &&!visited[poll[0]][poll[1] + 1]){
            queue.add(new int[]{poll[0],poll[1]+1});
            visited[poll[0]][poll[1]+1]=true;
        }
    }
    return count;
}
//计算数位和
public int sums(int x,int y){
    int ans=0;
    while (x != 0) {
        ans+=x%10;
        x/=10;
    }
    while (y != 0) {
        ans+=y%10;
        y/=10;
    }
    return ans;
}

时间复杂度：O(mn) 最坏情况，遍历矩阵。

空间复杂度：O(mn)

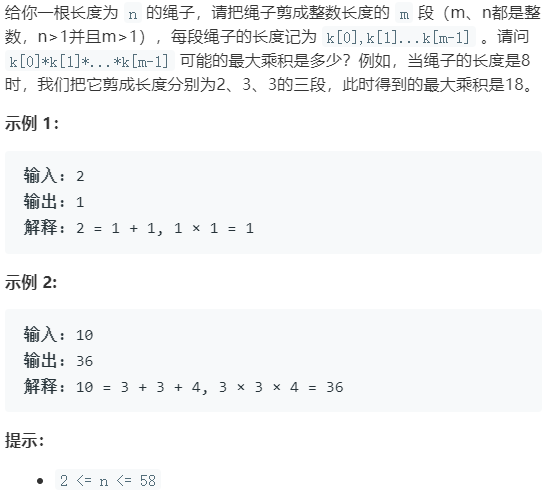
剑指Offer.14_I 剪绳子中等

思路一：动态规划 dp[i]数组的含义：长度为 i 的绳子剪断后可以得到的最大乘积。

初始化：dp[1]=dp[2]=1，即长度为 1 和 2 的绳子最大乘积是 1 。

状态转移：dp[i] = Max(dp[i],Max((i-j)*j,dp[i-j]*j))，遍历 [3,n] 长度的绳子，每种绳子都有j∈[0,i) 个位置可以进行剪断，剪断分为两种方式：1. 只在 j 位置剪断一次，得到乘积 (i-j)*j 。2. 将剪断后的部分 (i-j) 继续剪断，并选择可以形成最大的乘积方法 dp[i-j] ，所以是 dp[i-j]*j 。从两种方式里选最大的。

//时间复杂度：O(n^2)  空间复杂度：O(n)
public int cuttingRope(int n) {
    int[] dp = new int[n + 1];
    //初始化
    dp[1]=dp[2]=1;
    //[3,n] 种不通长度的绳子
    for (int i = 3; i < n + 1; i++) {
        //每个绳子有 [0,i) 个可剪断的位置
        for (int j = 0; j < i; j++) {
            dp[i] = Math.max(dp[i],Math.max((i-j)*j,j*dp[i-j]));
        }
    }
    return dp[n];
}

优化动态规划 学习自 @Krahets 的题解中（我并没有购买这本神书）。

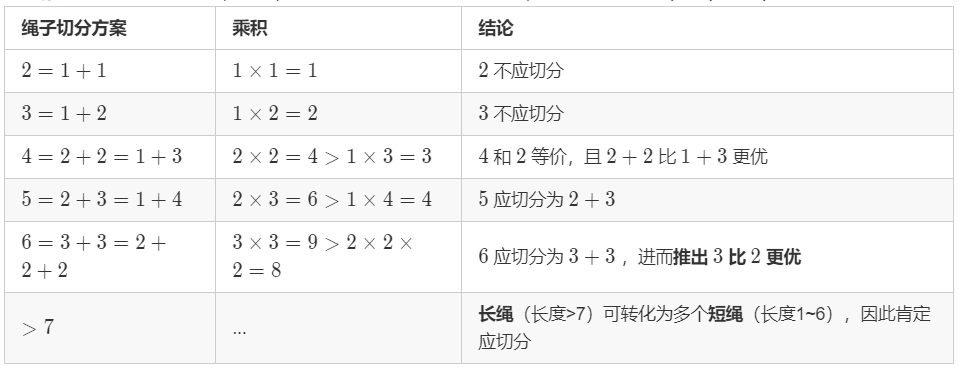
为使乘积最大，只有长度为 2 和 3 的绳子不应再切分，且 3 比 2 更优（详情见下表）

//时间复杂度：O(n)  空间复杂度：O(n)
public int cuttingRope(int n) {
    if (n < 4) return n - 1;
    int[] dp = new int[n + 1];
    dp[2] = 2;
    dp[3] = 3;
    for (int i = 4; i <= n; i++) {
        dp[i] = Math.max(2 * dp[i - 2], 3 * dp[i - 3]);
    }
    return dp[n];
}

剑指Offer.14_II 剪绳子II 中等

（一个更简单的办法，直接使用 BigDecimal 大数类型，方法不变和上一题一样。）

上题的优化解法，已经基本给出了本题的思路。本题的变化在于 n 的取值更大，可能出现整形溢出的情况。

思路一：贪心算法 我们首先考虑对于一段长n的绳子，我们可以切出的结果包含什么？

1 会包含吗？不会，因为 1 * (k - 1) < k , 只要把 1 和任何一个其他的片段组合在一起就有个更大的值

2 可以

3 可以

4 可以吗？它拆成两个 2 的效果和本身一样，因此也不考虑

5 以上可以吗？不可以，这些绳子必须拆，因为总有一种拆法比不拆更优，比如拆成 k / 2 和 k - k / 2

综上, 最后的结果只包含 2 和 3 (当然当总长度为 2 和 3 时单独处理), 那么很显然 n >= 5 时， 3*(n - 3) >= 2 * (n - 2) ，因此我们优先拆成 3 ，最后剩余的拆成 2 。最后的结果一定是由若干个 3 和 1 或 2 个 2 组成。

//时间复杂度：O(logn) 空间复杂度：O(1)
public int cuttingRope(int n) {
    if (n<4) return n-1;
    long res = 1;
    while (n > 4) {
        res *= 3;
        res %= 1000000007;
        n -= 3;
    }
    //别忘了最后一段绳子，长度 n
    return (int) (res*n%1000000007);
}

剑指Offer.15 二进制中 1 的个数简单

思路一：逐位统计 用 & 运算得到最后一位是 1 还是 0，每次统计完将 n 用 >>> 无符号右移 1 位。

public int hammingWeight(int n) {
    int count = 0;
    for (int i = 0; i < 32; i++) {
        count += n & 1;
        n >>>= 1;
    }
    return count;
}

思路二：减 1 统计 看例子：

n = 11010001
n = (n - 1)&n = 11010000 & 11010001 = 11010000
n = (n - 1)&n = 11001110 & 11010000 = 11000000
n = (n - 1)&n = 10111111 & 11000000 = 10000000
n = (n - 1)&n = 01111111 & 10000000 = 00000000 = 0
共计算了 4 次，得到结果：有 4 个 1 。

实现这个方式，每次计算之后计数器 +1 ，直至 n 变为 0，则统计完成。

public int hammingWeight(int n) {
    int count = 0;
    while (n != 0) {
        count++;
        n &= (n - 1);
    }
    return count;
}

剑指Offer.16 数值的整数次方中等

思路一：暴力法 这道题暴力法是不能通过leetcode判题机，会得到一个t。但是方法本身是可以得到正确答案的，所以我们需要对他进行优化。暴力法的想法很简单的：2^3=2*2*2。

如果n为负，则n=-n同时x=1/x，例如2^(-3)=1/2*1/2*1/2。但是这里要注意n的取值范围，主要是正整数和负整数的不同范围限制。

public double myPow(double x, int n) {
    if (x==0)return 0;
    if (n==0)return 1;
    double ans=1;
    long N=n;
    if (N<0){
        N=-N;
        x=1/x;
    }
    for (int i=0;i<N;i++){
        ans*=x;
    }
    return ans;
}

时间复杂度：O(n)

思路二：二分法 当我们得到x^(n/2)的时候，我们不需要再去乘上n/2个x了，而是x^(n/2)*x^(n/2)=x^n。

这个想法用递归很容易实现，但是需要注意的是n的奇偶性，如果n为奇数则需要再乘上一个x。

public double myPow(double x, int n) {
    switch (n){
        case 1:return x;
        case 0:return 1;
        case -1:return 1/x;
    }
    double half=myPow(x,n/2);
    //奇偶性处理
    double rest=myPow(x,n%2);
    return half*half*rest;
}

时间复杂度：O(logn)

剑指Offer.17 打印从 1 到最大的 n 位数简单

思路一：幂运算 上一题刚搞过幂运算，直接拿来用。n 位数的需要申请 10^n-1 大小的数组。

//时间复杂度：O(10^n)
public int[] printNumbers(int n) {
    int size = myPow(10, n);
    int[] res = new int[size - 1];
    //打印从 1 到 10^n-1
    for (int i = 0; i < res.length; i++) {
        res[i] = i + 1;
    }
    return res;
}

private int myPow(int x, int n) {
    switch (n) {
        case 1:
            return x;
        case 0:
            return 1;
        case -1:
            return 1 / x;
    }
    int half = myPow(x, n / 2);
    int rest = myPow(x, n % 2);
    return half * half * rest;
}

剑指Offer.18 删除链表的节点简单

思路一：遍历 cur 指针遍历链表，同时用一个 pre 指针指向 cur 节点的前驱， cur 指针找到 val 节点之后，删除 cur 节点即可。

//时间复杂度：O(n)
public ListNode deleteNode(ListNode head, int val) {
    if (head == null) return head;
    if (head.val == val) return head.next;
    ListNode cur = head.next, pre = head;
    while (cur != null) {
        if (cur.val != val) {
            cur = cur.next;
            pre = pre.next;
        } else {
            pre.next = cur.next;
            break;
        }
    }
    return head;
}

剑指Offer.19 正则表达式匹配困难

思路一：回溯法 这种匹配思路其实就是不断地减掉s和p的可以匹配首部，直至一个或两个字符串被减为空的时候，根据最终情况来得出结论。

如果只是两个普通字符串进行匹配，按序遍历比较即可：

1	if( s.charAt(i) == p.charAt(i) )

如果正则表达式字符串p只有一种”.”一种特殊标记，依然是按序遍历比较即可：

1	if( s.charAt(i) == p.charAt(i) \|\| p.charAt(i) == '.' )

上述两种情况实现时还需要判断字符串长度和字符串判空的操作。

但是，”*“这个特殊字符需要特殊处理，当p的第i个元素的下一个元素是星号时会有两种情况：

i元素需要出现0次，我们就保持s不变，将p的减掉两个元素，调用isMatch。例如s：bc、p：abc，我们就保持s不变，减掉p的”a\“，调用isMatch(s:bc,p:bc)。
i元素需要出现一次或更多次，先比较i元素和s首元素，相等则保持p不变，s减掉首元素，调用isMatch。例如s：aabb、p：abb，就保持p不变，减掉s的首元素，调用isMatch(s:abb,p:a\bb)。

此时存在一些需要思考的情况，例如s：abb、p：a*abb，会用两种方式处理：

按照上述第二种情况比较i元素和s首元素，发现相等就会减掉s的首字符，调用isMatch(s:bb,p:a*abb)。在按照上述第一种情况减去p的两个元素，调用isMatch(s:bb,p:abb)，最终导致false。
直接按照上述第一种情况减去p的两个元素，调用isMatch(s:abb,p:abb)，最终导致true。

所以说这算是一种暴力方法，会将所有的情况走一边，看看是否存在可以匹配的情况。

public boolean isMatch(String s, String p) {
    //如果正则串p为空字符串s也为空这匹配成功，如果正则串p为空但是s不是空则说明匹配失败
    if (p.isEmpty())return s.isEmpty();
    //判断s和p的首字符是否匹配，注意要先判断s不为空
    boolean headMatched=!s.isEmpty()&&(s.charAt(0)==p.charAt(0)||p.charAt(0)=='.');
    if (p.length()>=2&&p.charAt(1)=='*'){//如果p的第一个元素的下一个元素是*
        //则分别对两种情况进行判断
        return isMatch(s,p.substring(2))||
            (headMatched&&isMatch(s.substring(1),p));
    }else if (headMatched){//否则，如果s和p的首字符相等
        return isMatch(s.substring(1),p.substring(1));
    }else {
        return false;
    }
}

时间复杂度：O((n+m)*2^(n+m/2)) n和m分别是s和p的长度

思路二：动态规划法 本题的dp数组的含义就是：dp[i][j]就是s的前i个元素是否可以被p的前j个元素所匹配。

我们知道了dp数组的含义之后就知道了dp数组的几个细节：

dp[0][0]一定是true，因为s为空且p也为空的时候一定是匹配的；dp[1][0]一定是false，因为s有一个字符但是p为空的时候一定是不匹配的。
这个boolean类型的dp数组的大小应该是dp[s.length+1][p.length+1]，因为我们不仅仅要分别取出s和p的所有元素，还要表示分别取s和p的0个元素时候(都为空)的情况。
当写到dp[s.length][p.length]的时候，我们就得到了最终s和p的匹配情况。
dp[1][0]~dp[s.length][0]这一列都是false，因为s不为空但是p为空一定不能匹配。

所以创建好dp数组之后，初始化dp[0][0]=true、dp[0][1]=false、dp[1][0]~dp[s.length][0]都是false。然后将第一行即dp[0][2]到dp[0][p.length]的元素初始化。

第一行初始化思路：如果不为空的p想要匹配上为空的s，因为此时p已经不为空，则需要p是”a*“、”b*“、”c*“。。。这种形式的才能匹配上。

然后填写数组的其余部分，这个过程中如果p.charAt(j)==’*'依然是遵循上题中的两种情况；否则就判断两个字符串的i和j号字符是否相等，相等则分别减除当前字符继续判断，不相等则直接等于false。

public boolean isMatch(String s, String p) {
    //需要分别取出s和p为空的情况，所以dp数组大小+1
    boolean[][] dp=new boolean[s.length()+1][p.length()+1];
    //初始化dp[0][0]=true,dp[0][1]和dp[1][0]~dp[s.length][0]默认值为false所以不需要显式初始化
    dp[0][0]=true;
    //填写第一行dp[0][2]~dp[0][p.length]
    for (int k=2;k<=p.length();k++){
        //p字符串的第2个字符是否等于'*',此时j元素需要0个，所以s不变p减除两个字符
        dp[0][k]=p.charAt(k-1)=='*'&&dp[0][k-2];
    }
    //填写dp数组剩余部分
    for (int i=0;i<s.length();i++){
        for (int j=0;j<p.length();j++){
            //p第j个字符是否为*
            if (p.charAt(j)=='*'){
                //两种情况:1.s不变[i+1],p移除两个元素[j+1-2]。
                // 2.比较s的i元素和p的j-1(因为此时j元素为*)元素,相等则移除首元素[i+1-1],p不变。
                dp[i+1][j+1]=dp[i+1][j-1]||
                    (dp[i][j+1]&&headMatched(s,p,i,j-1));
            }else {
                //s的i元素和p的j元素是否相等,相等则移除s的i元素[i+1-1]和p的j元素[j+1-1]
                dp[i+1][j+1]=dp[i][j]&&headMatched(s,p,i,j);
            }
        }
    }
    return dp[s.length()][p.length()];
}
//判断s第i个字符和p第j个字符是否匹配
public boolean headMatched(String s,String p,int i,int j){
    return s.charAt(i)==p.charAt(j)||p.charAt(j)=='.';
}

时间复杂度：O(n*m) n和m分别是s和p的长度

有了第一题总结的”经验”之后，这道题逻辑上不难理解，但是细节上尤其各种下标值非常的恶心。

剑指Offer.20 表示数值的字符串中等

碍于篇幅，就赘述这种恶心人的题目了！

之前写过一篇博文专门记录过这道题：[LeetCode No.65]——什么是面向测试编程？看看本这道题就知道了！口区

剑指Offer.21 调整数组顺序使奇数位于偶数前面简单

思路一：双指针，快排变形 是 LeetCode NO.75 颜色分类中变形三路快排思路的简化版。双指针，分别找顺序第一个偶数，和逆序第一个奇数，然后交换，一次遍历即可完成交换。

//时间复杂度：O(n)
public int[] exchange(int[] nums) {
    int i = 0, j = nums.length - 1;
    while (i < j) {
        //顺序找第一个偶数
        while (i<j&&(nums[i]&1)==1)i++;
        //逆序找第一个奇数
        while (i<j&&(nums[j]&1)==0)j--;
        //交换位置
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
    return nums;
}

剑指Offer.22 链表中倒数第 k 个节点简单

用两个指针 slow、fast 分别指向链表的开头(哑节点)。
先让 fast 指针逐步移动到距离 slow 指针 k 的位置上，也就是上 slow 指针和 fast 指针 n 个间隔。
让 slow 指针和 fast 指针同时向后移动，直至 fast 指针为 null。
此时 slow 指针指向的就是倒数第 k 个节点。

//时间复杂度：O(n)
public ListNode getKthFromEnd(ListNode head, int k) {
    ListNode fast = head, slow = head;
    for (int i = 1; i <= k; i++) {
        fast = fast.next;
    }
    while (fast != null) {
        fast = fast.next;
        slow = slow.next;
    }
    return slow;
}

剑指Offer.24 翻转链表简单

思路一：三指针迭代 curr 指向当前待翻转的节点、pre 指向前驱、next 记录后继。

//时间复杂度：O(N)
public ListNode reverseList(ListNode head) {
    ListNode curr = head, pre = null;
    while (curr != null) {
        ListNode next = curr.next;
        curr.next = pre;
        pre = curr;
        curr = next;
    }
    return pre;
}

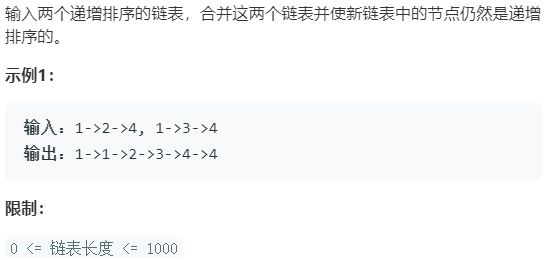
剑指Offer.25 合并两个排序的链表简单

思路一：遍历 遍历比较每个节点，根据节点大小，连接成一个新链表。最后不要忘了，较长链表的剩余部分直接拼接在新链表尾部。

//时间复杂度：O(n)    较短的那个链表长度为 n
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
    ListNode dummy = new ListNode(-1);
    ListNode p = dummy;
    while (l1 != null && l2 != null) {
        if (l1.val <= l2.val) {
            p.next = l1;
            l1 = l1.next;
        } else {
            p.next = l2;
            l2 = l2.next;
        }
        p = p.next;
    }
    p.next = l1 != null ? l1 : l2;
    return dummy.next;
}

本人菜鸟，有错误请告知，感激不尽！

更多题解源码和学习笔记：github 、CSDN 、M1ng

剑指Offer.13 机器人的运动范围 中等

思路一：深搜

思路二：广搜

剑指Offer.14_I 剪绳子 中等

剑指Offer.14_II 剪绳子II 中等

剑指Offer.15 二进制中 1 的个数 简单

剑指Offer.16 数值的整数次方 中等

剑指Offer.17 打印从 1 到最大的 n 位数 简单

剑指Offer.18 删除链表的节点 简单

剑指Offer.19 正则表达式匹配 困难

剑指Offer.20 表示数值的字符串 中等

剑指Offer.21 调整数组顺序使奇数位于偶数前面 简单

剑指Offer.22 链表中倒数第 k 个节点 简单

剑指Offer.24 翻转链表 简单

剑指Offer.25 合并两个排序的链表 简单