LeetCode——环形链表问题

NO.141 环形链表 简单、NO.142 环形链表II 中等 、NO.202 快乐数 简单 、NO.287 寻找重复数 中等

NO.141 环形链表 简单

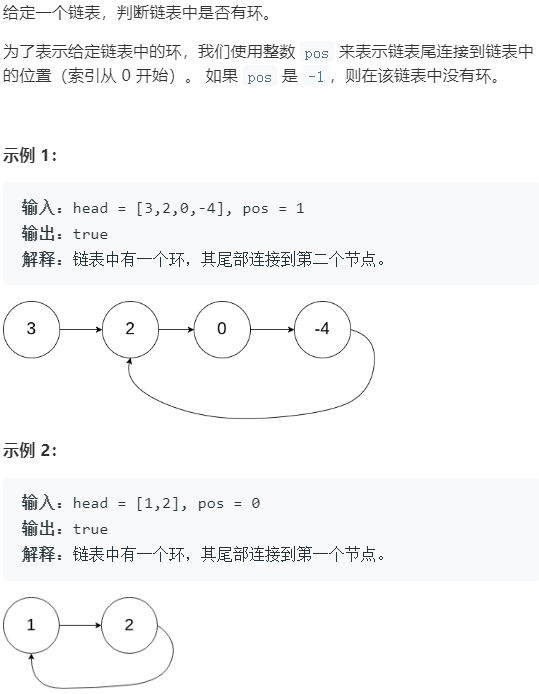
在NO.202快乐数中也有对以下两个思路相同的应用。

思路一：HashSet p指针遍历链表，将每个节点存入 set ，如果访问的节点 set 中存在，说明有环。

时间复杂度：O(n) 空间复杂度：O(n)

思路二：快慢指针 其实就是 Floyd 算法，如果快指针走到了结尾，说明不是环形链表；如果是环形链表快慢指针一定会相遇，因为入环之后每次移动快慢指针，就相当于让两个指针的距离 -1 。

public boolean hasCycle(ListNode head) {
    if (head == null || head.next == null) return false;
    ListNode fast = head.next, slow = head;
    while (fast != null && fast.next != null) {
        //相遇说明有环
        if (fast == slow) return true;
        fast = fast.next.next;
        slow = slow.next;
    }
    return false;
}

时间复杂度：O(n) 空间复杂度：O(1)

NO.142 环形链表II 中等

和其姊妹题NO.141的解题思路一样，稍微一些调整变化。

思路一：HashSet p指针遍历链表，将每个节点存入 set ，如果访问的节点 set 中存在，说明有环并返回此时的节点p。线性遍历，第一次重复一定是入环的第一个节点。

public ListNode detectCycle(ListNode head) {
    if (head == null || head.next == null) return null;
    HashSet<ListNode> set = new HashSet<>();
    ListNode p = head;
    while (p != null) {
        if (set.contains(p)) {
            return p;
        }
        set.add(p);
        p = p.next;
    }
    return null;
}

时间复杂度：O(n) 空间复杂度：O(n)

思路二：快慢指针 快慢指针如何进行不在赘述。重点在于如何找到入环的第一个节点。

先看一下最终实现：如果快指针遍历完成，没有环；

如果有环，当快慢指针第一次相遇后，慢指针原地不动，重置快指针回到表头节点，此时快慢指针都保持每次移动一个节点，当快慢指针第二次相遇的时候，此时相遇节点就是入环的第一个节点。

public ListNode detectCycle(ListNode head) {
    ListNode fast = head, slow = head;
    while (true) {
        //无环
        if (fast == null || fast.next == null) return null;
        fast = fast.next.next;
        slow = slow.next;
        //第一次相遇
        if (slow == fast) break;
    }
    //重置fast
    fast = head;
    //第二次相遇
    while (slow != fast) {
        slow = slow.next;
        fast = fast.next;
    }
    return slow;
}

时间复杂度：O(n) 空间复杂度：O(1)

为什么两次相遇一定是入环的第一个节点？

设链表有环，且链表共有 a+b 个节点，其中 链表头部到链表入口 有 a 个节点（不计链表入口节点）， 链表环 有 b 个节点；设两指针分别走了 f，s 步，则有：

1. fast 走的步数是slow步数的 2 倍，即 f = 2s ；
2. fast 比 slow多走了 n 个环的长度，即 f = s + nb ； ( 双指针都走过一次非环的部分 a 步，然后在环内绕圈直到重合，重合时 fast 比 slow 多走 环的长度整数倍 n )
3. 以上两式相减得：f = 2nb，s = nb，即fast和slow 指针分别走了 2n，n 个 环的周长 。

如果一个指针 k 遍历这个有环链表一次需要走 k = a + nb 步 (此时 n=1)，此时 k 会回到入环节点。

而目前，slow 指针走过的步数为 nb 步。因此，我们只要想办法让 slow 再走 a 步停下来，就可以到环的入口节点。

但是此时我们并不知道参数链表的 a 是多少！

所以让 fast 和 slow 第一次相遇后(此时 s = nb)，fast 从头节点开始每次走一步，同时 slow 也在环内每次走一步，当 fast 走 a 步到达入环节点时，slow 共走了 s = a + nb 步，即 slow 也到达入环节点。

所以只需要第二次 fast 和 slow 相遇即可，此时一定是在入环节点。

NO.202 快乐数 简单

思路一：HashTable 用一个 HashSet 对每一个数字的每一位求平方相加，结果 num 如果是 1 则说明 n 是快乐数；如果不是 1，判断 HashSet 中是否已经存在相同的 num，如果存在说明出现闭环，不存在则结果放入 Set 并继续按位平方求和，判断结果。

public boolean isHappy(int n) {
    HashSet<Integer> set = new HashSet<>();
    //还没有证明n是快乐数,也没有发生循环
    while (n != 1 && !set.contains(n)) {
        set.add(n);
        n = helper(n);
    }
    return n == 1;
}
//按位平方求和
private int helper(int n) {
    int num = 0;
    while (n > 0) {
        int temp = n%10;
        num+=temp*temp;
        n/=10;
    }
    return num;
}

不需要考虑平方求和之后的结果num超出范围，因为 999 的结果是 243 、9999 的结果 324 、、、 9999999999999 的结果 1053 。。。发现，三位数最大的按位平方求和结果还是个三位数，所以无论怎么求下去，都是三位数。

时间复杂度：O(logn) 空间复杂度：O(n)

思路二：快慢指针 不断地生成 num ，num 生成下一个 num ，这是一种链式的递减，如果链上的某个节点出现了 1 ，说明 n 是快乐数，如果链上出现了环，说明 n 不是快乐数。

这种思路下，本问题就转换成了判断链表是否有环的问题，在判断的途中顺便检测是否有节点为 1 。

慢指针一次走一个节点，快指针一次走两个节点，如果存在循环，那么快慢一定会相遇。

public boolean isHappy(int n) {
    int slow = n, fast = helper(n);
    while (fast != 1 && slow != fast) {
        slow = helper(slow);
        fast = helper(helper(fast));
    }
    return fast == 1;
}

//按位平方求和
private int helper(int n) {
    int num = 0;
    while (n > 0) {
        int temp = n % 10;
        num += temp * temp;
        n /= 10;
    }
    return num;
}

时间复杂度：O(logn) 空间复杂度：O(1)

NO.287 寻找重复数 中等

思路一：快慢指针 读完题并不能立刻想到判环问题。如果将数组建图，下标位置 i 都有一个连接 nums[i] 的边。本题说有且只有一个重复元素 num，那么 num 这个位置至少有两条边指向他，所以图里一定有环，而这个重复元素 num 就是环的入口。

问题变成了找环的入口问题，就变成了上面的 NO.142 环形链表 II。区别仅在于本题是数组而已。

依然快慢指针，虽然本题不是一个链表，但是根据前面所说的建图后有了链表的性质(下标 i -> nums[i])，所以移动一步就是 slow = nums[slow]，同样的走两步就是 fast = nums[nums[fast]] 。

public int findDuplicate(int[] nums) {
    int slow = 0, fast = 0;
    while (true) {
        slow = nums[slow];
        fast = nums[nums[fast]];
        //第一次相遇
        if (slow == fast) break;
    }
    //重置一个指针,快慢指针都每次一个步长
    slow = 0;
    while (slow != fast) {
        slow = nums[slow];
        fast = nums[fast];
    }
    //第二次相遇就是环入口
    return slow;
}

时间复杂度：O(n) 空间复杂度：O(1)

---

本人菜鸟，有错误请告知，感激不尽！

更多题解源码和学习笔记：github 、CSDN 、M1ng